Натурален логаритъм

Натуралният логаритъм (на латински: logarithmus naturalis) или естествен логаритъм е логаритъм с основа математическата константа $e=2{,}718281828459...$. Числото „$e$“ е ирационално и се дефинира като границата на (1+1/n)ⁿ при n, клонящо към безкрайност:

Графика на натуралния логаритъм

$e=\lim _{n\,\to \,\infty }\,\left(1+{\frac {1}{n}}\right)^{n}$.

Натуралният логаритъм от $x$ е степента, на която $e$ трябва да се повдигне, за да бъде равно на $x$. Ако $x=e^{y}$, тогава $y=\ln x$. Естественият логаритъм от $e$ е равен на 1, тъй като $e$¹ = $e$, а eстественият логаритъм от 1 е 0, тъй като $e$⁰ = 1.

Натуралният логаритъм от $x$ обикновено се записва като ln x или log_e x. По-рядко може да бъде записан и без означаване на основата, само като log x. Понякога се добавят скоби за яснота: ln(x), log_e(x) или log(x).

Естественият логаритъм ln(x) е дефиниран за всички реални положителни стойности на $x$, както и за всички ненулеви комплексни стойности. Въпреки че не е въведена от Джон Непер, тази функция понякога се нарича неперов логаритъм, а числото $e$ се нарича неперово число.

По теоремата на Линдеман-Вайерщрас натуралният логаритъм на всяко едно положително алгебрично число без 1 е трансцендентно число.

Определения

Натуралният логаритъм може да се дефинира по няколко еквивалентни начина.

Обратна функция на експонентата

Натуралният логаритъм може да се дефинира като обратна функция на експоненциалната функция с равенствата:

$e^{\ln(x)}=x\qquad {\mbox{ако }}x>0\,\!$

$\ln(e^{x})=x.\,\!$

С други думи, той е биекция на множеството на реалните положителни числа върху множеството на всички реални числа, а още по-прецизно погледнато, той е изоморфизъм между групата на реалните положителни числа относно умножението и групата на реалните числа относно събирането:

$\ln :(\mathbb {R} ^{+},\times )\to (\mathbb {R} ,+)$

ln(a) илюстриран като площта под кривата f(x) = 1/x от 1 до а. Ако стойността на а е по-малка от 1, площта от а до 1 е отрицателна.

Интегрална дефиниция

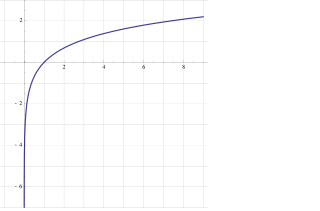
Формално ln(a) може да се дефинира като областта под графиката на функцията ${\frac {1}{x}}$ от 1 до $a$, която се дава с интеграла

$\ln(a)=\int _{1}^{a}{\frac {1}{x}}\,dx.$

Той дефинира логаритъма, тъй като удовлетворява основното свойство на логаритмите:

$\ln(ab)=\ln(a)+\ln(b)\,\!$

Това може да се покаже чрез заместването $t={\tfrac {x}{a}}$ по следния начин:

$\ln(ab)=\int _{1}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{a}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{t}}\;dt=\ln(a)+\ln(b)$

История

Идеята за натуралния логаритъм е разбработена от Гегоар дьо Сан-Винсент и Алфонс Антонио де Сараса преди 1649 г. Тяхната работа включва квадратура на хиперболата xy = 1 чрез определяне площта на хиперболичните сектори. Тяхното решение генерира необходимата функция на хиперболичния логаритъм, притежаваща свойства, свързани с натуралния логаритъм.

Едно от най-ранните споменавания на натуралния логаритъм е от Николас Меркатор в работата си Logarithmotechnia, публикувана през 1668 г., въпреки че през 1619 г. учителят по математика Джон Спейдъл вече е бил съставил таблица на натурални логаритми.

Конвенции за обозначения

Обозначенията ln x и log_e x се отнасят недвусмислено до натуралния логаритъм от $x$, а log x без означена основа може също да се отнася до натуралния логаритъм. Тази употреба е често срещана в математиката, заедно с някои научни контексти, както и в много езици за програмиране. Обаче в някои други контексти, като например химия, log x може да се използва за обозначаване на десетичния логаритъм (с основа 10). Може също да се отнася до двоичния логаритъм (с основа 2) в контекста на компютърните науки, особено в контекста на времевата сложност. В калкулаторите log x може да означава една от двете функции десетичен или натурален логаритъм – другата съответно е означена с еднозначния си символ ln x или lg x.

Площта под хиперболата удовлетворява логаритмичния закон. Тук A(s,t) означава площта под хиперболата между s и t.

Свойства

• $\ln 1=0$
• $\ln e=1$
• $\ln(xy)=\ln x+\ln y\quad {\text{за }}\;x>0\;{\text{и }}\;y>0$
• $\ln(x^{y})=y\ln x\quad {\text{за }}\;x>0$
• $\ln x<\ln y\quad {\text{за }}\;0<x<y$
• $\lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1$
• $\lim _{\alpha \to 0}{\frac {x^{\alpha }-1}{\alpha }}=\ln x\quad {\text{за }}\;x>0$
• ${\frac {x-1}{x}}\leq \ln x\leq x-1\quad {\text{за}}\quad x>0$
• $\ln {(1+x^{\alpha })}\leq \alpha x\quad {\text{за}}\quad x\geq 0\;{\text{и }}\;\alpha \geq 1$

Вижте също

• Логаритъм на матрица
• Интегрален логаритъм
• Полилогаритъм
• Функция на Манголд
• Неперово число
• Николас Меркатор