Сортиране по метода на гребена

Сортирането по метода на гребена е прост алгоритъм за сортиране, първоначално разработен от Владимир Добошевич през 1980 г. По-късно алгоритъмът е преоткрит от Стефан Ласи и Ричард Бокс през 1991 г. Алгоритъмът на гребена подобрява метода на мехурчето.

Пример как методът сортира една редица

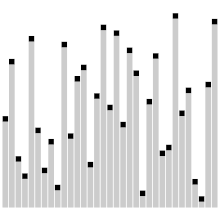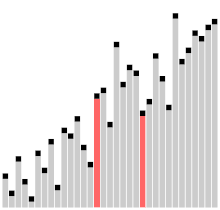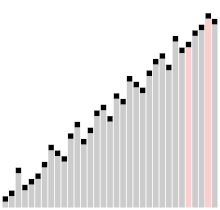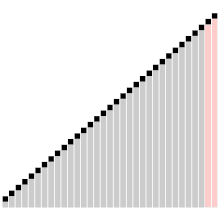
Алгоритъм

Костенурки и зайци

Големите елементи в началото на последователността не представляват трудност за алгоритъма, защото бързо се нареждат на съоветната позиция и от там идва и името им зайци, но малките елементи в края се пренареждат изключително бавно (костенурки).

Основната идея на метода е да елиминира костенурките или малките стойности близо до края на масива, което е и главната причина за сериозното забавяне в метода на мехурчето. Големите стойности в началото (зайците) не представляват проблем за метода на мехурчето.

Когато кои да са два елемента биват сравнявани в метода на мехурчето, гапът (разликата или още отдалечеността между елементите) винаги е 1. Основната идея на сортирането по метода на гребена е, че гапът би могъл да бъде и повече от 1 (Методът на Шел също е базиран на тази идея, но той се смята по скоро за развитие на сортирането чрез вмъкване).

С други думи, вътрешният цикъл на метода на мехурчето, който в действителност извършва размяната, е конструиран така, че гапът между разменените елементи да намалява (за всяко следващо влизане във външния цикъл).

Принцип на действие

1. Алгоритмът започва, като една променлива (обикновено се нарича “gap”), получена като дължината на масива, който предстои да бъде сортиран, се разделя на т.нар. стесняващ фактор, чиято стойност обикновено е 1.3, се сортира според получената стойност, която се закръгля към цяло число, ако се налага.
2. След това променливата(„gap“) се разделя отново на стесняващия фактор, масивът се сортира отново и това продължава, докато въпросната променлива не стане със стойност 1.
3. Последната стъпка на масива е еквивалентна на метода на мехурчето, но костенурките, които толкова го забавят, вече са наредени.

Стесняващ фактор

Стесняващият фактор (на английски: shrink factor) има доста голям ефект върху производителността на метода. В първоначалната статия авторът е предложил да бъде 1,3. Стойност, която едновременно е малка, за да забави алгоритъма, с цел да се извършат всички сравнения и твърде голяма, за да не забавя прекалено метода. Ласи и Бокс експериментално установяват (тествайки над 200 000 произволни масива), че най-подходящата стойност за стесняващия фактор е 1,3.

Имплементация на метода

C#

using System;

class ShellSort
{
 static void Main()
 {
 int[] array = {123,212,12,46,54,21,1,78};
 sort(array);
 }

 static int newGap(int gap)
 { 
 gap = (int)(gap / 1.3);
 if(gap == 9 || gap == 10)
 gap = 11;
 if(gap < 1)
 return 1;
 return gap;
 }
 
 static void sort(int[] arr)
 { 
 int gap = arr.Length;
 bool swapped;
 do
 {
 swapped = false;
 gap = newGap(gap);
 for (int i = 0; i < (arr.Length – gap); i++)
 {
 if (arr[i] > arr[i + gap])
 {
 swapped = true;
 int temporary = arr[i];
 arr[i] = arr[i + gap];
 arr[i + gap] = temp;
 }
 }
 }
 while (gap > 1 || swapped);
 }
}

C++

int newGap(int gap)
{
 gap /= 1.3;
 if (gap == 9 || gap == 10)
 gap = 11;
 if (gap < 1)
 return 1;
 return gap;
}

void sort(int arr[], int length)
{
 int gap = length;
 bool swapped;
 do
 {
 swapped = false;
 gap = newGap(gap);
 for (int i = 0; i < length – gap; ++i)
 {
 if (arr[i] > arr[i + gap])
 {
 swapped = true;
		int temporary = arr[i];
		arr[i] = arr[i + gap];
		arr[i + gap] = temporary;
 }
 }
 } 
 while (gap > 1 || swapped);
}

Java

private static int newGap(int gap)
{ 
	gap = gap / 1.3;
 if(gap == 9 || gap == 10)
 gap = 11;
 if(gap < 1)
 return 1;
 return gap;
}
 
private static void sort(int arr[])
{ 
	int gap = arr.length;
 boolean swapped;
 do
 { 
		swapped = false;
 gap = newGap(gap);
 for(int i = 0; i < (arr.length – gap); i++)
 { 
			if(arr[i] > arr[i + gap])
 { 
				swapped = true;
 int temporary = arr[i];
 arr[i] = arr[i + gap];
 arr[i + gap] = temp;
 }
 }
 } 
	while(gap > 1 || swapped);
}