Задача с две тела

В класическата механика, задачата с две тела се използва за определяне на движението на две точкови частици, които си взаимодействат само помежду си. Като пример за това може да се отбележи спътник, обикалящ около планета, планета, обикаляща около звезда, две звезди, обикалящи една около друга (двойна звезда), и класически електрон, обикалящ около атомно ядро (макар за да се реши последната задача правилно е нужен подхода на квантовата механика).

Ляво: Две тела със сходна маса орбитират около общ барицентър (външен за двете тела) с елиптични орбити, характерни за двойните звезди.
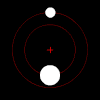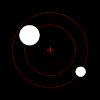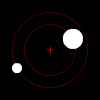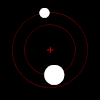
Дясно: Две тела с малка разлика в масата орбитират около общ барицентър. Размерите и този тип орбита са подобни на тези в системите Плутон-Харон (където барицентърът е външен за двете тела) и Земя-Луна (където барицентърът се намира в по-голямото тяло).

Задачата с две тела може да бъде формулирана като две отделни задачи с по едно тяло - една тривиална и една включваща решаване по отношение на движението на частица при наличието на външен потенциал. Тъй като много задачи с едно тяло могат да се решат с точност, съответно и задачата с две тела също може да бъде решена. За разлика от нея, задачата с три тела (и по-общо, задачата с n на брой тела) не може да бъде решена по отношение на първите интеграли, освен в частни случаи.

Намаляване до две независими задачи с по едно тяло

Координати на Якоби за задачата с две тела. Координатите са: ${\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}$ и ${\boldsymbol {r}}={\boldsymbol {x}}_{1}-{\boldsymbol {x}}_{2}$ при $M=m_{1}+m_{2}\$.

Нека x₁ и x₂ да са векторните позиции на двете тела, а m₁ и m₂ да са техните маси. Целта е да се определят траекториите x₁(t) и x₂(t) по всяко време t, след като са дадени началните местоположения x₁(t = 0) и x₂(t = 0) и началните скорости v₁(t = 0) и v₂(t = 0).

Когато се приложи за двете маси, вторият закон на Нютон гласи:

$\mathbf {F} _{12}(\mathbf {x} _{1},\mathbf {x} _{2})=m_{1}{\ddot {\mathbf {x} }}_{1}\quad \quad \quad (\mathrm {\ } 1)$

$\mathbf {F} _{21}(\mathbf {x} _{1},\mathbf {x} _{2})=m_{2}{\ddot {\mathbf {x} }}_{2}\quad \quad \quad (\mathrm {\ } 2)$

където F₁₂ е силата върху маса 1, поради взаимодействието ѝ с маса 2, а F₂₁ е силата върху маса 2, поради взаимодействието ѝ с маса 1. Двете точки над векторите x обозначават втората им производна спрямо времето, тоест векторите им на ускорение.

Събирането и изваждането на тези две уравнения ги разединява в две задачи с по едно тяло, които могат да бъдат решени поотделно. След събирането на уравненията (1) и (2) се получава уравнение, описващо барицентричното движение. Изваждането на уравнение (2) от уравнение (1) води до уравнение, което описва как векторът r = x₁ − x₂ между масите се променя с времето. Решенията на тези независими задачи могат да се комбинират, за да се получат решенията на траекториите x₁(t) и x₂(t).

Център на движение на масата

Нека $\mathbf {R}$ да е местонахождението на центъра на масите в системата. Събирането на уравненията на силата (1) и (2) дава:

$m_{1}{\ddot {\mathbf {x} }}_{1}+m_{2}{\ddot {\mathbf {x} }}_{2}=(m_{1}+m_{2}){\ddot {\mathbf {R} }}=\mathbf {F} _{12}+\mathbf {F} _{21}=0$

където се използва третия закон на Нютон F₁₂ = −F₂₁ и където

${\ddot {\mathbf {R} }}\equiv {\frac {m_{1}{\ddot {\mathbf {x} }}_{1}+m_{2}{\ddot {\mathbf {x} }}_{2}}{m_{1}+m_{2}}}.$

Полученото уравнение

${\ddot {\mathbf {R} }}=0$

показва, че скоростта V = dR/dt на центъра на масите е постоянна, от което следва, че общият импулс m₁ v₁ + m₂ v₂ също е постоянен. Оттук, местоположението R (t) на центъра на масите може да се определи във всяко време от началните местоположения и скорости.

Векторно движение на изместване

Разделяйки двете уравнения на силата със съответните маси, изваждането на второто уравнение от първото и пренареждане дава уравнението:

${\ddot {\mathbf {r} }}={\ddot {\mathbf {x} }}_{1}-{\ddot {\mathbf {x} }}_{2}=\left({\frac {\mathbf {F} _{12}}{m_{1}}}-{\frac {\mathbf {F} _{21}}{m_{2}}}\right)=\left({\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}\right)\mathbf {F} _{12}$

където отново се използва третия закон на Нютон F₁₂ = −F₂₁ и където r е векторът на преместване от маса 2 до маса 1.

Силата между двата обекта, която произлиза от тях, трябва да е само функция на тяхното разделяне r, а не на техните абсолютни позиции x₁ и x₂. В противен случай не би имало транслационна симетрия и законите на физиката биха били нарушени. Изваденото уравнение може да бъде записано така:

$\mu {\ddot {\mathbf {r} }}=\mathbf {F} _{12}(\mathbf {x} _{1},\mathbf {x} _{2})=\mathbf {F} (\mathbf {r} )$

където $\mu$ е приведената маса

$\mu ={\frac {1}{{\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}}}={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}.$

Решаването на уравнението за r(t) е ключът към задачата с две тела. След като R (t) и r(t) са определени, първоначалните траектории могат да се получат чрез:

$\mathbf {x} _{1}(t)=\mathbf {R} (t)+{\frac {m_{2}}{m_{1}+m_{2}}}\mathbf {r} (t)$

$\mathbf {x} _{2}(t)=\mathbf {R} (t)-{\frac {m_{1}}{m_{1}+m_{2}}}\mathbf {r} (t)$

което може да бъде проверено чрез заместването на R и r в тези уравнения.

Планарно движение

Движението на две тела едно спрямо друго винаги лежи в една равнина, която е част от референтната система на центъра на масата.

Доказателство: определянето на линейния импулс p и момента на импулса L на системата спрямо центъра на масата чрез уравненията

$\mathbf {L} =\mathbf {r} \times \mathbf {p} =\mathbf {r} \times \mu {\frac {d\mathbf {r} }{dt}},$

където μ е приведената маса, а r е относителната позиция r₂-r₁, показва, че скоростта на промяна на момента на импулса L е равна на момента на сила N

$\mathbf {N} ={\frac {d\mathbf {L} }{dt}}={\dot {\mathbf {r} }}\times \mu {\dot {\mathbf {r} }}+\mathbf {r} \times \mu {\ddot {\mathbf {r} }}\ ,$

Може да се използва свойството на векторното произведение v × w = 0 за всички вектори v и w, ориентирани в една и съща посока

$\mathbf {N} \ =\ {\frac {d\mathbf {L} }{dt}}=\mathbf {r} \times \mathbf {F} \ ,$

като F = μ d ²r / dt ².

Ако се допусне, че силата между двете частици действа по дължина на линията между техните местоположения (вярно за повечето физически сили, тъй като се подчиняват на Третия закон на Нютон), тогава r × F = 0, а векторът на момента на импулса L е постоянен (запазен). Следователно, този вектор на преместване r и скоростта му v винаги се намират в равнина, която е перпендикулярна постоянния вектор L.

Енергия на системата

Ако силата F(r) е консервативна, тогава системата има потенциална енергия U(r), така че общата енергия може да бъде записана като:

$E_{\text{tot}}={1 \over 2}m_{1}{\dot {\mathbf {x} }}_{1}^{2}+{1 \over 2}m_{2}{\dot {\mathbf {x} }}_{2}^{2}+U(\mathbf {r} )={1 \over 2}(m_{1}+m_{2}){\dot {\mathbf {R} }}^{2}+{1 \over 2}\mu {\dot {\mathbf {r} }}^{2}+U(\mathbf {r} )$

В отправната система на барицентъра, кинетичната енергия е най-малка и общата енергия става:

$E={1 \over 2}\mu {\dot {\mathbf {r} }}^{2}+U(\mathbf {r} )$

Координатите x₁ и x₂ могат да се изразят така:

$\mathbf {x} _{1}={\frac {\mu }{m_{1}}}\mathbf {r}$

$\mathbf {x} _{2}=-{\frac {\mu }{m_{2}}}\mathbf {r}$

и по подобен начин енергията E е свързана с енергиите E₁ и E₂, които поотделно съдържат кинетичната енергия на всяко тяло:

${\begin{aligned}E_{1}&={\frac {\mu }{m_{1}}}E={1 \over 2}m_{1}{\dot {\mathbf {x} }}_{1}^{2}+{\frac {\mu }{m_{1}}}U(\mathbf {r} )\\[4pt]E_{2}&={\frac {\mu }{m_{2}}}E={1 \over 2}m_{2}{\dot {\mathbf {x} }}_{2}^{2}+{\frac {\mu }{m_{2}}}U(\mathbf {r} )\\[4pt]E_{\text{tot}}&=E_{1}+E_{2}\end{aligned}}$