Ротация (диференциален оператор)

Ротàция, завѝхряне или рòтор във векторния анализ е векторен диференциален оператор над векторно поле.

Обозначава се по няколко начина:

• $\operatorname {rot}$ (най-разпространено в рускоезични източници, а също и в немския, откъдето е произлязло наименованието.
• $\operatorname {curl}$ (в англоезичната литература, предложено е от Джеймс Кларк Максуел.
• $\mathbf {\nabla } \times$ – диференциален оператор набла, векторно умножен по векторно поле $\mathbf {A}$. Резултатът от действието на оператора „ротация“ върху конкретно векторно поле $\mathbf {A}$ се нарича „ротация на полето $\mathbf {A}$“ или просто „ротация от $\mathbf {A}$“ и представлява ново векторно поле $\mathbf {\nabla } \times \mathbf {A}$.

$\operatorname {rot} \mathbf {A} \equiv \mathbf {\nabla } \times \mathbf {A}$

Определяне на посоката на вектора на ротацията (извивката). Свитите 4 пръста на дясната ръка сочат посоката на въртене ${\hat {\omega }}$ на векторното поле $A$, а палецът показва посока на вектора на извивката ${\hat {n}}=\operatorname {rot} \mathbf {A}$.

Ротацията представлява безкрайно малко въртене на векторно поле в триизмерното евклидово пространство. Във всяка точка на векторното поле извивката около точката се изразява като вектор, наречен вектор на извивката. Свойствата (дължина и посока) на този вектор характеризират въртенето в тази точка.

Посоката на завихрянето е оста на въртене, която се определя от правилото на дясната ръка, а големината на завихрянето е количеството на въртене. Ако векторното поле представлява скоростта на потока на движещ се ротор, тогава завихрянето е плътността на циркулационната площ на ротора. Векторно поле с нулево извиване се нарича иротационно векторно поле. Ротацията е диференциална форма на вектор. Противоположността на фундаменталната теорема на смятането е теоремата на Стокс, която свързва повърхностния интеграл на завихрянето на векторно поле с криволинейния интеграл на това векторно поле около гранична крива.

За разлика от градиента и дивергенцията, ротацията не просто се обобщава към други измерения; възможно е известно обобщение, но само в три измерения, където геометрично дефинираното векторно поле на ротацията все още е векторно поле. Това явление е подобно на триизмерното кръстосано произведение и тази връзка е отразена в символа на завихрянето $\mathbf {\nabla } \times$.

Името „завихряне“ ($\operatorname {curl}$) за ротация е предложено за първи път от Максуел през 1871 г. , но концепцията очевидно е използвана за първи път във формулирането на теорията на оптичното поле на Джеймс МакКълах през 1839 г.

Компонентите на вектора F(r) на разстояние r, нормалата ${\hat {n}}$ и допирателната към затворената крива C в равнината и векторната площ A = An̂, затворена от тази крива.

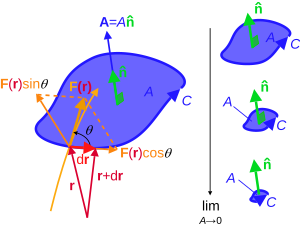
Определение

За да се дефинира завихрянето (ротацията) на векторно поле, първо трябва да се въведе понятието циркулация (или вихър). Дадено е векторно поле $\mathbf {A}$ в триизмерно пространство и проста затворена насочена крива $C$, циркулацията на $\mathbf {A}$ по кривата $C$ е криволинеен интеграл от $\mathbf {A}$ по затворения път $C$:

$\operatorname {Circ} _{\mathbf {A} }(C)=\oint _{C}\mathbf {A} \cdot \mathrm {d} {\boldsymbol {l}}$ ,

където $\mathrm {d} {\boldsymbol {l}}$ е линеен елемент на кривата $C$ по допирателната към нея, а положителната ѝ посока е определена така, че площта, оградена от затворената крива $C$ е от лявата му страна. Например, ако има водовъртеж в посока обратна на часовниковата стрелка в реката на брега на реката, тогава в обхвата на водовъртежа водният поток се върти около центъра на водовъртежа, така че скоростта на водата ${\boldsymbol {v}}$ следва затворена крива около вихъра обратно на часовниковата стрелка. Интегралът трябва да е по-голям от нула, т.е. циркулацията е по-голяма от нула. Това показва, че полето на скоростта на водния поток във вихъра се върти в кръгове в обхвата на вихъра.

Циркулацията, подобно на потока, е важен параметър за описание на векторно поле. Циркулацията в дадена област не е равна на нула, което означава, че векторното поле в тази област проявява характеристиката да се върти около определена точка или определена област. Ротацията е начин да се опише това свойство локално. За да се опише циркулацията на векторно поле $\mathbf {A}$ близо до точка, се избира малък повърхностен елемент $\Delta S$, включващ тази точка и се разглежда циркулацията на векторното поле $\mathbf {A}$ по дължината на граничната крива $C$. Когато повърхностният елемент $\Delta S$ се свие и площта $\left|\Delta S\right\vert$ клони към нула, векторното поле $\mathbf {A}$ е по протежение на пръстена и повърхностния елемент на $C$. Граничната стойност на съотношението на циркулацията на векторното поле $\mathbf {A}$ по контура $C$ към площта, заградена от него на панела $\Delta S$ е

$\lim _{\Delta S\to 0}{\frac {1}{\left|\Delta S\right\vert }}\oint _{C}\mathbf {A} \cdot \mathrm {d} {\boldsymbol {l}}$ .

Нарича се плътност на циркулационната площ, повърхностна плътност на циркулация или сила на циркулация на векторното поле $\mathbf {A}$. Очевидно, тъй като посоката [Забележка 2], избрана от повърхностния елемент $\Delta S$ е различна, получената плътност на циркулационната площ също се изменя. За да се покаже степента на въртене на векторното поле в близост до точка, трябва да се покаже неговата максимална възможна стойност и посоката, избрана от съответния сърфел. Завихрянето на векторно поле е вектор. Размерът на неговата проекция в една посока представлява размерът на повърхностната плътност на пръстена в тази посока. Тоест ротацията на $\mathbf {A}$ в една точка се записва като $\mathbf {rot\,} \mathbf {A} (x)$ или $\mathbf {curl\,} \mathbf {A} (x)$:

$\mathbf {rot\,} \mathbf {A} (x)\cdot \mathbf {n} =\lim _{\Delta S_{\mathbf {n} }\to 0}{\frac {1}{\left|\Delta S_{\mathbf {n} }\right\vert }}\oint _{C_{\mathbf {n} }}\mathbf {A} \cdot \mathrm {d} {\boldsymbol {l}}$ .

Тук $\Delta S_{\mathbf {n} }$ се отнася до повърхностния елемент, чийто нормален вектор е единичният вектор $\mathbf {n}$ и има неговата посока, а $C_{\mathbf {n} }$ е граничната крива на елемента. Ако се представи от оператора набла ${\boldsymbol {\nabla }}$, ротацията на векторното поле $\mathbf {A}$ се записва $\operatorname {rot} \mathbf {A} =\mathbf {\nabla } \times \mathbf {A}$. Може да се види от дефиницията, че ротацията е свойство на интензитет на векторното поле, точно като плътност, концентрация и температура, и съответното му свойство на разширение е векторното поле по обиколката по затворена крива, така че извивката е повърхностната плътност на циркулацията. Ако извивката навсякъде във векторно поле е нула, полето се нарича иротационно поле или консервативно поле.

Правоъгълна координатна система

Нека в триизмерната правоъгълна (декартова) координатна система $xyz$ векторното поле $\mathbf {A}$ е

$\mathbf {A} (x,y,z)=A_{x}(x,y,z)\mathbf {i} +A_{y}(x,y,z)\mathbf {j} +A_{z}(x,y,z)\mathbf {k}$，

където $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ са единични вектори съответно в посоките на òсите $x$,$y$, $z$ и компонентите на полето $A_{x},A_{y},A_{z}$ имат непрекъснати частни производни от първи ред, тогава проекциите върху всяка координатна ос са:

${\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}},\quad {\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}},\quad {\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}$.

Векторът на ротацията се нарича още кривина на векторното поле $\mathbf {A}$ и се записва в основната форма

$\mathbf {rot\,} \ \mathbf {A} ={\boldsymbol {\nabla }}\times \mathbf {A} =\left({\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)\mathbf {k}$

Изразът за ротацията може също да бъде изразен в детерминантна нотация:

$\mathbf {rot\,} \mathbf {A} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\A_{x}&A_{y}&A_{z}\end{vmatrix}}$

Трябва да се отбележи, че нотацията на детерминантата тук има само формално значение, тъй като коефициентите в реалната детерминанта трябва да бъдат стойности вместо векторите $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$. Този метод на представяне е удобен само за запаметяване на израза за ротацията в декартовата координатна система.

Цилиндрична координатна система

В цилиндричната координатна система позицията на обекта се определя от две линейни $(z,\rho )$ и една ъглова $(\varphi )$ координати: напречните са $\rho ,\varphi$, а надлъжната е $z$. Те определят неговите единични вектори: напречен радиален ${\boldsymbol {e}}_{\rho }$, напречен азимутален ${\boldsymbol {e}}_{\varphi }$ и надлъжен ${\boldsymbol {e}}_{z}$. Тогава векторът на полето $\mathbf {A}$ има компоненти $A_{\rho },A_{\varphi },A_{z}$ и може да се изрази като:

$\mathbf {A} =A_{\rho }(\rho ,\varphi ,z){\boldsymbol {e}}_{\rho }+A_{\varphi }(\rho ,\varphi ,z){\boldsymbol {e}}_{\varphi }+A_{z}(\rho ,\varphi ,z){\boldsymbol {e}}_{z}$ ,

а ротацията (извивката) на векторното поле е

$\mathbf {rot\,} \mathbf {A} =\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right){\boldsymbol {e}}_{\rho }+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\boldsymbol {e}}_{\varphi }+{\frac {1}{\rho }}\left({\frac {\partial ({\rho }A_{\varphi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\boldsymbol {e}}_{z}$ .

Сферична координатна система

В сферичната координатна система позицията на обекта се определя от една линейна $(r)$ и две ъглови координати (азимут $\varphi$ и ъгъл на място $\theta$). Те определят неговите единични вектори: ${\boldsymbol {e}}_{r}$, ${\boldsymbol {e}}_{\varphi }$ и ${\boldsymbol {e}}_{\theta }$. Векторът на полето $\mathbf {A}$ има компоненти $A_{r},A_{\varphi },A_{\theta }$ и може да се изрази като:

$\mathbf {A} =A_{r}(r,\varphi ,\theta ){\boldsymbol {e}}_{r}+A_{\varphi }(r,\varphi ,\theta ){\boldsymbol {e}}_{\varphi }+A_{\theta }(r,\varphi ,\theta ){\boldsymbol {e}}_{\theta }$ .

Аналогично ротацията на векторното поле се определя от израза

$\mathbf {rot\,} \mathbf {A} ={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\varphi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \varphi }}\right){\boldsymbol {e}}_{r}+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\boldsymbol {e}}_{\varphi }+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {\partial (rA_{\varphi })}{\partial r}}\right){\boldsymbol {e}}_{\theta }\,.$