Център на масите
Център на масите се нарича геометричната точка в тяло или система от частици, която характеризира движението на масата в системата, разглеждана като едно цяло. Нарича се още център на инерцията или точка на равновесие и е позицията на среднопретеглената маса на тялото, в която сумата от масите на всички негови точки е равна на нула.

Нека една механична система се състои от тела с маси , които могат да се разглеждат като материални точки с радиус-вектори съответно . Точката, определена с радиус-вектора
- ,
където се изменя от 1 до , се нарича център на масите на системата. Движението на системата като цяло под действие на външни сили, чиято равнодействаща е , може да се разглежда като движение на материална точка с маса и радиус-вектор , върху която е приложена сила . Пълният импулс на системата следователно може да се представи като произведение на и скоростта на движение на центъра на масите. За непрекъснато разпределение на масите в една механична система радиус-векторът на центъра на масите се дава с израза
- ,
където е законът, по който се изменя плътността на масите, а интегрирането е по обема , който заема системата.
Често за изследване на кинематиката на ансамбли от частици се използва т.нар. координатна система на центъра на масите, чието начало е в центъра на масите и е неподвижно по дефиниция (скоростта му на движение е 0).[1]
Център на тежестта редактиране
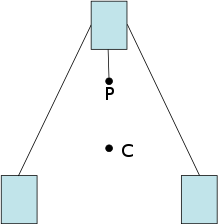
Центърът на тежестта на механичната система е точката, по отношение на която общият момент на силите на тежестта (действащи върху системата) е равен на нула. Например, в система, състояща се от две еднакви маси, свързани с негъвкав прът и поставени в нехомогенно гравитационно поле (например планети), центърът на масата ще бъде в средата на пръта, докато центърът на тежестта на системата ще бъде изместена към този край на пръта, който е по-близо до планетата (тъй като теглото G = m·g зависи от параметъра на гравитационното поле g и, най-общо казано, дори се намира извън пръта.
В еднородно гравитационно поле центърът на тежестта винаги съвпада с центъра на масата. В некосмически задачи гравитационното поле обикновено може да се счита за постоянно в обема на тялото, така че на практика тези два центъра почти съвпадат.
По същата причина понятията център на масата и център на тежестта съвпадат, когато тези термини се използват в геометрията, статиката и други подобни области, където тяхното приложение в сравнение с физиката може да се нарече метафорично и където неявно се предполага ситуацията на тяхната еквивалентност (тъй като няма реално гравитационно поле, то и отчитането на неговата хетерогенност няма смисъл). При тези употреби двата термина традиционно са синоними и често вторият се предпочита просто защото е по-стар. [1]
Полезно е да се отбележи, че центърът на масата е фиксирано свойство за дадено твърдо тяло (напр. без плискане или артикулация), докато центърът на тежестта може в допълнение да зависи от неговата ориентация в неравномерно гравитационно поле. В последния случай центърът на тежестта винаги ще бъде разположен малко по-близо до основното привлекателно тяло в сравнение с центъра на масата и по този начин ще промени позицията си в интересуващото ни тяло, когато се промени неговата ориентация.
При изучаването на динамиката на въздухоплавателни средства, превозни средства и плавателни съдове, силите и моментите трябва да бъдат разделени спрямо центъра на масата. Това е вярно независимо от това дали се отчита гравитацията. Назоваването на центъра на масата като център на тежестта е нещо като разговорен език, но е често срещано и когато ефектите на гравитационния градиент са незначителни, центърът на тежестта и центърът на масата са едни и същи и се използват взаимозаменяемо.
Във физиката ползите от използването на центъра на масата за моделиране на разпределението на масата могат да се видят чрез разглеждане на резултата от действието на силите на гравитацията върху непрекъснато тяло. Разгледа се тяло Q с обем V и плътност ρ(r) във всяка точка r от обема. В паралелно гравитационно поле силата f във всяка точка r се дава от израза
където dm е масата в точката r, g е ускорението на гравитацията и е единичен вектор, определящ вертикалната посока.
Избира се референтна точка R в обема и се изчислява резултантната сила F и въртящия момент M в тази точка:
иАко референтната точка R е избрана така, че да е центърът на масата, тогава
Чрез избирането на центъра на тежестта като отправна точка за твърдо тяло, силите на гравитацията няма да накарат тялото да се върти, което означава, че теглото на тялото може да се счита за концентрирано в центъра на масата.
Вижте също редактиране
Литература редактиране
- Бобылёв Д. К. – Центр, в физике, ВТ-ЭСБЕ.
- Журавлёв В. Ф. – Основы теоретической механики. 2-е изд., 320 стр., ISBN 5-94052-041-3, М., Физматлит, 2001.
- Die Physik: ein Lexikon der gesamten Schulphysik. Schülerduden, Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01122-X, S. 367–368.
- Marion, Jerry B. – Dinámica clásica de las partículas y sistemas, ISBN 84-291-4094-8, Ed. Reverté, Barcelona, 1996.
- Ortega, Manuel R.|título – Lecciones de Física (4 volúmenes), ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7, editorial „Monytex“, 1989-2006.
- Resnick, Robert & Krane, Kenneth S. – Physics, ISBN 0-471-32057-9, John Wiley & Sons, New York, 2001.
- Serway, Raymond A. & Jewett, John W. – Physics for Scientists and Engineers, 6ª ed., ISBN 0-534-40842-7, Brooks/Cole, 2004.
- Tipler, Paul A.|título – Física para la ciencia y la tecnología (2 volúmenes), ISBN 84-291-4382-3, Reverté, Barcelona, 2000.
Източници редактиране
- ↑ а б Тарг С. М. – Центр инерции (центр масс), Физическая энциклопедия, 5, стр. 624—625.











