Дзета-функция на Риман

Дзета-функцията на Риман, означавана като , е обобщение за сумирането на безкрайни редове от дроби. Тя носи името на немския математик Бернхард Риман. Функцията е от особена важност в теорията на числата поради връзката ѝ с разпределението на простите числа. Тя също има приложения във физиката,[1] в теорията на вероятностите и в статистиката.
Дефиниция
редактиране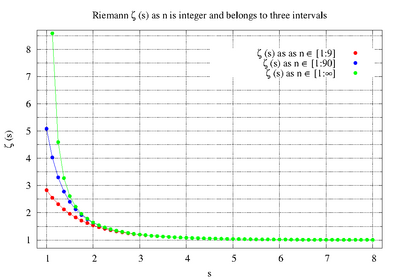
Дзета-функцията на Риман ζ(s) е функция на една комплексна променлива (традиционно отбелязвана със s), която се дефинира посредством следния безкраен ред:
Този ред е ред на Дирихле и е сходящ за всички реални числа s> 1. Функцията може да се додефинира за всички комплексни s ≠ 1 с помощта на аналитично продължение. Риман показва това в статията си „Относно броя на простите числа по-малки от дадено число“ през 1859 година. Той прави това на две стъпки. Първо Риман показва че редът е сходящ за всички комплексни s с реална част Re(s) по-голяма от 1 и дефинира аналитична функция на променливата s в областта {s ∈ C: Re(s) > 1} След това той показва как да продължи ζ(s) за всички комплексни s различни от 1. В резултат дзета-функцията се превръща в мероморфна функция на s, която е холоморфна в областта {s∈C:s≠ 1} и има прост полюс в s=1. Аналитичното продължение дефинира еднозначно функцията ζ(s) извън първоначалната област на сходимост. В допълнение на това, Риман извежда и функционално уравнение за дзета-функцията, което дава връзка между стойността ѝ в точките s и 1 − s. Известната хипотеза на Риман, която е формулирана в същата статия се отнася за нулите на така продължената функция. За да се подчертае, че s е комплексно число, то често се записва във вида s=σ + it, където σ = Re(s) е реалната, а t = Im(s) – имагинерната част на s.
Отношение към простите числа
редактиранеОйлер пръв открива връзката между сумите от дроби и простите числа. Впоследствие неговите резултати се записват чрез дзета функцията. Той открива формулата
където отдясно стои безкрайно произведение по всички прости числа p. Това произведение е сходящо за Re(s) > 1. То е следствие на два основни резултата в математиката: формулата за геометрична прогресия и основната теорема на аритметиката.
Свойства
редактиранеСтойности в зададени точки
редактиранеСледните числа са най-често използваните стойности на дзета-функцията на Риман.
- ; това е
- .
- ; Това число се нарича константа на Апери.
За положителните четни числа е валидна формулата
където , а са числата на Бернули.
За отрицателните цели числа е валидна следната формула
за .
, когато k е нечетно и по-голямо от 1, от където следва, че
тоест четните отрицателни цели числа са нули (корени) на дзета-функцията. Тези нули се наричат тривиални нули. Стойностите за първите няколко отрицателни нечетни числа са
Това са фактически аналитични продължения, които позволяват да се приписват определени стойности на неограничено растящи стандартни сумирания. Така например
Също стойността на дзета-функцията за e .
Функционално уравнение
редактиранеДзета-функцията удоволетворява следното функционално уравнение:
което е изпълнено за всички комлпексни числа s освен 0 и 1. Тук, с Γ е обозначена гама-функцията. Тази формула се използва за построяване на аналитичното продължение на дзета-функцията. В точката s = 1, функцията има прост полюс с резидуум 1. Равенството също показва, че дзета-функцията има нули в точките −2, −4. Това са така наречените тривиални нули.
Съществува и симетричен вариант на функционалното уравнение. Той се получава като първо се дефинира функцията
Тогава функционалното уравнение се задава чрез формулата
Нули
редактиранеДзета-функцията на Риман има нули в отрицателните цели числа. Това са така наречените тривиални нули.
Те са тривиални в смисъл, че тяхното съществуване може да се докаже сравнително лесно (например използвайки функционалното уравнение). Всички останали нули се наричат нетривиални. Нетривиалните нули са обект на много по-голямо внимание, не само защото тяхното разпределение е много по-слабо изучено, но и защото информация за тях дава отговори на забележително много въпроси от различни области на математиката. Известно е че всички нетривиални нули лежат в отворената ивица {s ∈ C: 0 < Re(s) < 1}, която се нарича критичната ивица. Хипотезата на Риман, която се смята за един от най-важните нерешени проблеми в математиката, твърди, че за всяка нетривиална нула s е вярно Re(s) = 1/2. В теорията на дзета-функцията на Риман, множеството {s ∈ C: Re(s) = 1/2} се нарича критичната права.
Местоположението на нулите на дзета-функцията е от огромна важност за теорията на числата. От факта, че всички нетривиални нули лежат в критичната ивица може да се изведе законът за разпределение на простите числа. Най-добрия известен резултат за областта в която се намират критичните нули[2] е, че ζ(σ+it) ≠ 0 ако |t| ≥ 3 и
Този резултат е неизмеримо по-слаб от твърдението на римановата хипотеза. Той дори не гарантира, че съществува ивица {s ∈ C: ε ≤ Re(s) ≤ 1-ε} извън която дзета-функцията да няма нули.
Известно е, че има безброй много нули върху критичната права. Литълууд показва, че ако редицата (γn) се състои от имагинерните части на всички нули в горната полу-равнина в нарастващ ред, то
Теоремата за критичната права твърди, че положителен процент от нулите лежи върху критичната права.
Нулата с най-малка неотрицателна имагинерна част в критичната ивица е 1/2+i14,13472514… От функционалното уравнение може да се види, че множеството на нетривиалните нули е симетрично относно правата Re(s) = 1/2. Също така от факта, че ζ(s)=ζ(s*)* за всички комплексни s ≠ 1 (* означава комплексно спрягане) следва, че нулите на дзета-функцията са симетрични относно реалната права.
Реципрочна функция
редактиранеРеципрочната функция на дзета-функцията на Риман може да се изрази като ред на Дирихле с коефициенти функцията на Мьобиус μ(n):
за всяко комплексно число s с реална част > 1.
Обобщения
редактиранеИзвестен брой дзета-функции могат да бъдат считани за обобщения на дзета-функцията на Риман. Един такъв пример е дзета-функцията на Хурвиц
която съвпада с дзета-функцията на Риман когато q = 1. Други примери са L-функциите на Дирихле и дзета-функцията на Дедекинд.
Външни препратки
редактиране- Riemann Zeta Function, в Wolfram Mathworld – Математическо насочено изложение на английски































